专业笔记

Terminology Index

IQA：图像质量评价，image quality assessment

上游任务，预训练模型，对应 low-level task；下游任务，具体的 task，对应 high-level task

Ablation study：消融实验，移除 Model 的部分"feature"（控制变量法），对比研究模型的性能

FPS：每秒传输帧数，frames per second

Fine-tune：微调，Fine tune a network

Ground truth：真实值

Feature map：特征图，一般指CNN中卷积层的输出

Pipline：流水线，论文中用其表示（翻译）方法or模型的框架

SOTA：State-of-the-art，译为：最先进的、最高水平

Off-the-shelf：译作：现成的、已经实现过的

Without bells and whistles：表示没有花里胡哨的东西/方法

Warm up：热身，由于网络初始化的参数一般是随机的，
故用一个小的学习率先训练几个epoch，防止一开始使用较大的学习率不稳定

光谱（Spectrum）：复色光经过分光成为单色光，经成像系统得到按波长或者频率依次排列的光学图像
多光谱（Multispectrum）：同时获取多个光学频谱波段（大于3个），在可见光基础上向红外、紫外两个方向扩展
高光谱（Hyperspectrum）：包含成百上千的波段，可以捕获和分析一片空间区域内“逐点”的光谱

Embedding：在深度学习中利用线性或非线性转换，对复杂的数据进行自动特征抽取，
并将其features表示为向量形式，以便于输入到网络中进行处理。这个过程被称之为"Embedding"

BN(Batch Normalization)：向深度学习模型输入数据时，要对data进行归一化操作，如均值为0、方差为1的规范化处理，
否则过大的特征会“淹没”小特征。这种情况不仅会在输入模型时出现，也会在层与层中存在，因为随着数据的逐级传播，
经过损失函数（如Softmax）后会使得特征之间的差异变大，逐渐累积会对最终结果造成较大的影响。
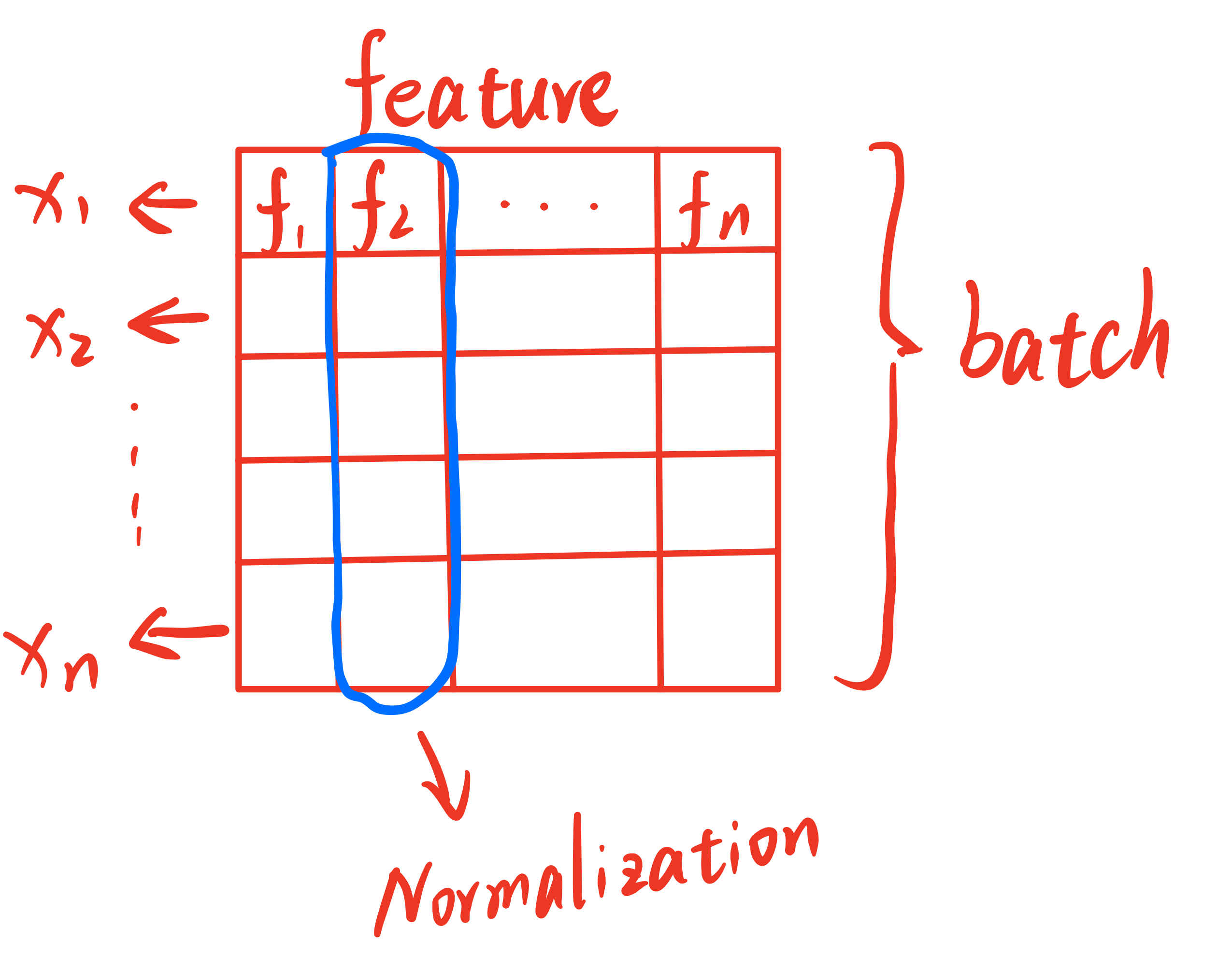
所以需要对层间数据也进行规范化，BN就是在两个隐藏层之间对数据在Batch方向进行Norm处理，
并且最后加入了Scale and Shift操作，以提高网络对Norm的学习能力。

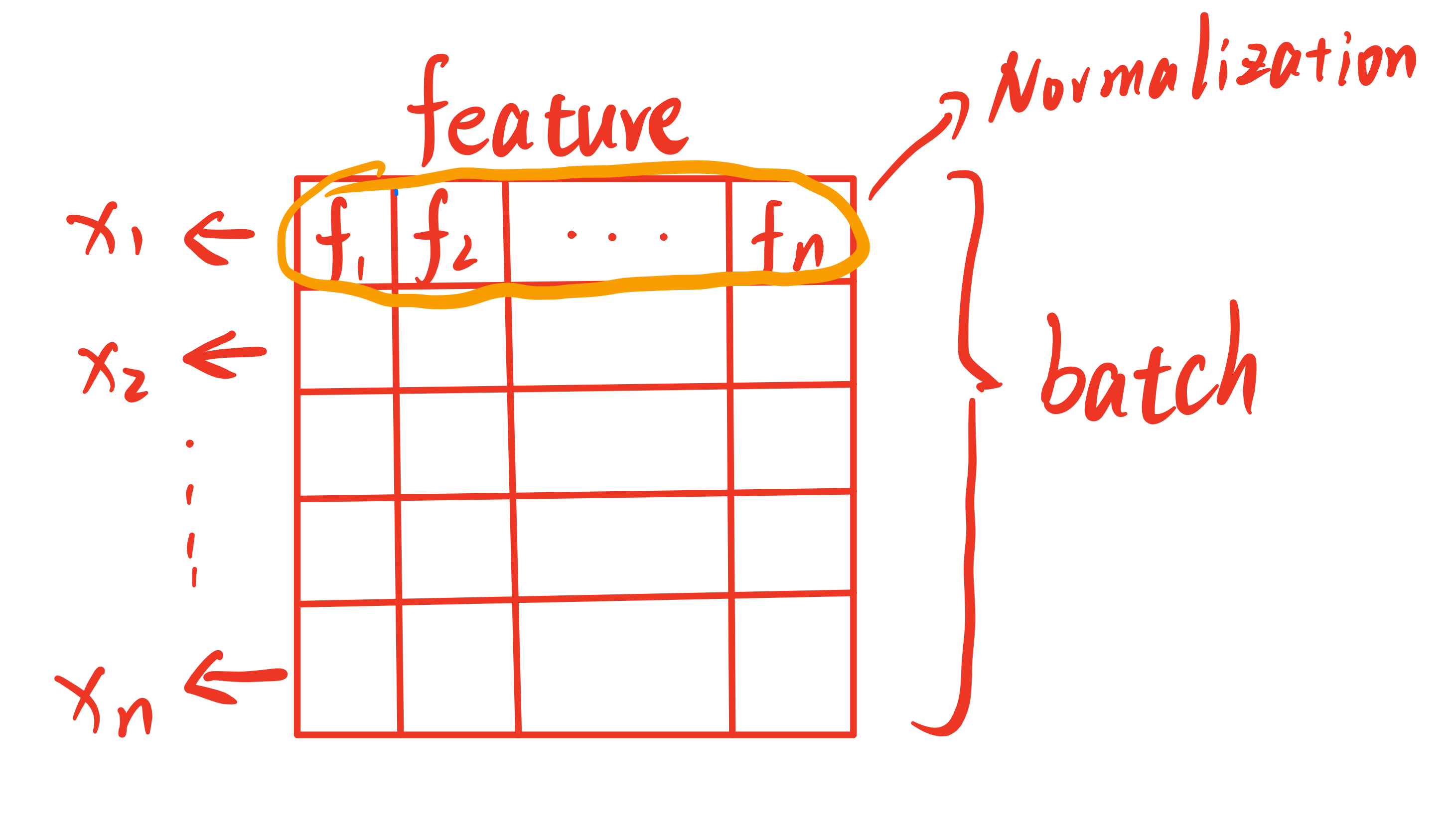
LN(Layer Normalization)：与BN不同之处在于，LN是在数据的Channel方向进行Norm归一化操作。
BN是对一个batch的数据的对应位置上所有的feature进行归一化，而LN是对每个sample进行归一化。
在三维视觉任务的情形下，可以理解为：BN对每一张图片对应位置的像素做Norm处理，LN则是对单幅图像的整体做Norm。
但通常在数据传入Model前会进行数据的归一化处理，因此通常不会再使用LN。

下面附上朋友博客的两张关于BN和LN的图，链接：https://emil-jiang.github.io

深度学习基本术语（补充）：

Batch：批，指使用训练集中的一小部分样本对模型权重进行一次反向传播的参数更新，这一小部分样本被称为“一批数据”，即一个batch。

Epoch：时代、纪元，使用训练集的全部数据对模型进行一次完整训练（前向计算+反向传播），称之为“一代训练”，即一个epoch。

Iteration：迭代，使用一个batch的数据对模型进行一次参数更新的过程，被称为“一次训练”，即一次iteration。

换算关系：Number of Batches = TrainingSet Size \(\div\) Batch Size.

如CIFAR10数据集有50000张训练图片，10000张测试图片。现在选择Batch_size = 256对模型进行训练。则：

• 每个epoch要训练的图片数量：50000
• 训练集具有的batch个数：50000 / 256 = 195 (余80) + 1 = 196
• 每个epoch需要完成的batch个数：196
• 每个epoch具有的iteration个数：196
• 每个epoch中模型权重更新的次数：196
• 训练10代后，模型权重更新的次数：196 \(\times\) 10 = 1960
• 最后一批数据（batch）的样本数：80
• 每一代训练（epoch）用的都是同一训练集的数据，但对模型的更新不同

迭代次数与epoch数密切相关。随着epoch数量的增加，权重更新迭代的次数增多，模型会由欠拟合（underfitting）状态，逐渐过渡到正常拟合状态，最后到达过拟合（overfitting）状态。epoch的设置一般与数据集的多样化程度有关，数据多样化程度越高，epoch越大。

论文中常见的缩写符号：

w/ : with（有），一般在消融实验的图表中，进行对照
w/o : without（没有），一般在消融实验的图表中，进行对照
w.r.t : with respect to的缩写，是“关于、谈及”的意思
i.e. : [that is, in other words] 源自拉丁语，译为：也就是、即
etc. : [and so forth, and others, and other things, and the rest, and so on, and such,
      and the like] et cetera的缩写，可追溯至拉丁语，意思是“等等”，用于列举事物的末尾
s.t. : subject to的简写，译为：受...的约束
e.g. : [for example, for instance, such as]
      源自拉丁语，英译：for example / for the sake of example，中译：举个例子、例如
cf. : 衍生自拉丁语，类似于reference，表示“比较、查阅、参考”之意
et al. : [and the others, and co-workers] 也是“等等”的意思，多用于人物之后
vanilla : 原意为“香草、香草味的”，引申含义是“普通的、原始的”，或“毫无特色的”
viz. : vidilicet, 译：即、就是。要把其前面的单词所包含的项目全部罗列出来才用这个缩写，
      与上述缩写词写法（"i.e.,"、"e.g.,"等）不同，其后面不用逗号。
      同：namely, to wit, that is to say, more precisely, more particularly, etc.

距离度量

欧氏距离（Euclidean Distance）：两点连线长度
城区距离（曼哈顿距离，Manhattan Distance）：直角移动距离，不涉及对角线
棋盘距离（切比雪夫距离，Chebyshev Distance）：沿某个轴的距离最大值
汉明距离（Hamming Distance）：比较两等长二进制串不同值的个数
余弦相似度（Cosine Similarity）：两向量夹角余弦表示距离，与内积有关

范数：

1.Norm of vector:

向量的范数

2.Norm of matrix:

若 \(A = (a_{ij})_{m \times n}\) ，则矩阵的诱导范数（算子范数）为：

p-范数：\(\Vert A \Vert _p = \mathop{max}\limits_{x \neq 0} \frac{\Vert Ax \Vert _p}{\Vert x \Vert _p}\)

L1范数（列和的最大值）：\(\Vert A \Vert_1 = \mathop{max}\limits_{1\le j \le n} \sum\limits_{i=1}^{m} \vert a_{ij} \vert\)

无穷范数（行和的最大值）：\(\Vert A \Vert_\infty = \mathop{max}\limits_{1\le i \le m} \sum\limits_{j=1}^{n} \vert a_{ij} \vert\)

L2范数（谱范数，当A为方阵时）：\(\Vert A \Vert_2 = \sqrt{\lambda_{max} (A^TA)}\)

矩阵\(A_{m \times n}\)的元范数（元素p-范数）：\(\Vert A \Vert _p = (\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n} \vert a_{ij} \vert ^p)^{\frac{1}{p}}\)

注：不要把矩阵元 p-范数与诱导 p-范数混淆。

对p = 2的元范数，称为弗罗贝尼乌斯范数（Frobenius norm）或希尔伯特-施密特范数（Hilbert–Schmidt norm），不过后面这个术语通常只用于希尔伯特空间。Frobenius-norm可用不同的方式定义： \[ \Vert A \Vert _F = \sqrt{\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n} \vert a_{ij} \vert ^2} = \sqrt{trace(A^{*} \cdot A)} = \sqrt{\sum\limits_{i=1}^{min\{m,n\}} \sigma _i^2} \] 其中\(A^{*}\)是\(A\)的共轭转置，\(\sigma _i\)是\(A\)的奇异值，\(trace()\)是迹函数。

Schaten范数出现于当元p-范数应用于一个矩阵的奇异值向量时。如果奇异值记做\(\sigma _i\)，则Schatten p-范数定义为： \[ \Vert A \Vert _F = \bigg(\sum\limits_{i=1}^{min\{m,n\}} \sigma _i^p \bigg)^{\frac{1}{p}} \]

TV范数：Total Variation，一种常用的正则项（距离度量），参考文章：如何理解全变分Distance

范数的等价需要一致范数的知识点，详情可以参考：各种矩阵范数总结

常用损失函数

1.Average

平均策略，包括算术平均和加权平均。

\(F(x,y) = \alpha _1 I_1(x,y) + \alpha _2 I_2(x,y)\)

2.Norm

Normalization，规范化，如L1-norm、L2-norm等，参考上面“距离度量”栏目内容。

Regularization，正则化，用于降低模型的复杂度，防止过拟合（Overfitting）问题。

L1正则主要用于特征选择，使其稀疏化，得到更多的零参数，\(R = \sum\limits_i{\vert w_{i} \vert}\)

L2正则主要用于求得更小的解（参数），防止过拟合，\(R = \sum\limits_i{\vert w_{i} \vert ^2}\)（平方惩罚力度更大）

3.MSE, RMSE and MAE

Mean Square Error，均方误差MSE，又称L2损失，\(Loss = \dfrac{1}{n} \sum\limits_{i = 1}^n (y_i - f(x_i))^2\)

Root Mean Square Error，均方根误差RMSE，\(Loss = \Big(\dfrac{1}{n} \sum\limits_{i = 1}^n (y_i - f(x_i))^2 \Big)^{\frac{1}{2}}\)

Mean Absolute Error，绝对值误差MAE，又称L1损失，\(Loss = \sum\limits_{i = 1}^n \vert y_i - f(x_i)\vert\)

4.KL散度

Kullback-Leibler divergence，也叫相对熵：relative entropy，用于衡量概率分布之间的距离。

\(Loss = \sum\limits_{i = 1}^n Y_i \cdot \log(\dfrac{Y_i}{F(x_i)})\)

5.交叉熵

Cross Entropy：Loss = \(-\sum\limits_{i = 1}^{n} Y_i \log F(x_i)\)

交叉熵损失函数刻画了模型实际输出概率与期望分布概率之间的相似程度，交叉熵的值越小，说明两个概率分布越接近。在二分类任务中存在正负样本不均衡问题时常用交叉熵作为损失函数（也称为对数损失函数），卷积神经网络在进行影像识别任务中最常使用的分类损失函数也是交叉熵损失函数，可以避免梯度消散问题。

激活函数建议搭配：tanh（双曲正切函数）、sigmoid函数（钻石函数）、ReLU函数（rectified linear unit，修正线性单元）、Softmax函数（Logistic的扩展，适用于多分类任务）。

tanh(x) = \(\dfrac{e^x - e^{-x}}{e^x + e^{-x}}\)，Sigmoid(x) = \(\dfrac{1}{1 + e^{-x}}\)，Relu(x) = \(\max(0,x)\)，Softmax(x) = \(\dfrac{e^{x_i}}{\sum\limits_{i} e^{x_i}}\)

6.对数似然

对数似然（likelihood）损失：\(L = -\dfrac{1}{n} \sum\limits_{i = 1}^n [y_i \log(p_i) + (1 - y_i) \log(1 - p_i)]\)

合页损失Hinge Loss：\(L = \max(0, \ 1-yf(x))\)

Huber Loss：\(L = \begin{cases} \frac{1}{2}(y - f(x))^2 \qquad \qquad \vert y - f(x)\vert \leq \delta \\ \delta \vert y - f(x) \vert - \frac{1}{2}\delta ^2 \qquad \vert y - f(x)\vert > \delta \end{cases}\)

7.PSNR

Peak Signal to Noise Ratio，峰值信噪比PSNR，\(L_{PSNR} = 10 \log(\dfrac{f_{max}^2}{L_{MSE}})\)

8.Perceptual Loss

感知损失，即图像感知相似度指标：Learned Perceptual Image Patch Similarity（LPIPS），该值越低，表示两张图像越相似。该损失是一个深度学习模型，输入为图像，输出感知相似性分数。

9.SSIM

SSIM是一种衡量图像结构相似性的算法，结合了图像的亮度，对比度和结构三方面对图像质量进行测量。SSIM的公式如下:

\(SSIM(x,y) = [L(x,y)]^{\alpha} \cdot [C(x,y)]^{\beta} \cdot [S(x,y)]^{\gamma}\)

L(x,y)是亮度部分：

\(L(x,y) = \dfrac{2\mu _x\mu _y + C_1}{\mu _x^2 + \mu _y^2 + C_1}\)

C(x,y)是对比度部分：

\(C(x,y) = \dfrac{2\sigma _x\sigma _y + C_2}{\sigma _x^2 + \sigma _y^2 + C_2}\)

S(x,y)是结构部分：

\(L(x,y) = \dfrac{\sigma _{xy} + C_3}{\sigma _x\sigma _y + C_3}\)

式子中，\(\mu _x\)与\(\mu _y\)是图像的像素平均值，\(\sigma _x\)和\(\sigma _y\)是图像的像素标准差，\(\sigma _{xy}\)是图像x和y的协方差，\(C_1\)、\(C_2\)、\(C_3\)是常数，防止分母等于0。一般情况下，\(\alpha = \beta = \gamma = 1\)，\(C_2 = 2\times C_3\)，则有：

\(SSIM(x,y) = \dfrac{(2\mu _x\mu _y + C_1)}{(\mu _x^2 + \mu _y^2 + C_1)}\cdot \dfrac{(2\sigma _{xy} + C_2)}{(\sigma _x^2 + \sigma _y^2 + C_2)}\)

10.TV损失

详见上面“距离度量”栏目范数部分所附链接。

图片格式

JPEG，静态图像压缩标准，压缩比越高，质量越差
JPG，与JPEG类似，相当于简化版，去除了相机的拍照参数等
PNG，无损压缩，位图片格式
GIF，静态、动态图像，如动图、表情包
TIFF，无失真压缩，占用空间较大
TGA，兼顾 BMP 图像的质量与 JPEG 的体积
BMP，位图 Bitmap，不采用压缩，占用空间大
SVG，二维矢量图形格式
RAW，经 CMOS 或 CCD 图像感应器将捕捉到的光信号转换为数字信号的原始数据
HDR，高动态范围图像，High-Dynamic Range，记录了照明信息

拓扑结构

什么是拓扑结构？

所谓“拓扑”，就是把实体抽象成与其大小、形状无关的“点”，把连接实体的线路抽象成“线”，进而以图的形式来表达这些点与线的关系。这个图被称为拓扑结构图，表示的关系是拓扑结构。

几何结构：强调点与线构成的形状及大小，考察点、线（甚至面）的位置关系。
拓扑结构：注重点、线之间的连接关系。

例子：梯形、矩形、平行四边形、圆具有不同的形状，因此属于不同的几何结构，但是组成它们的点、线连接关系是一样的，因此具有相同的拓扑结构（环形结构）。

在计算机网络中，我们把计算机、终端、通信处理机等设备抽象成点，把连接这些设备的通信线路抽象成线，其构成的拓扑叫网络拓扑结构，反应网络的结构关系。

几种常见的网络拓扑结构：总线型、星型、环型、树型、网状型等。

详情点击此处查看

线性代数基础知识

矩阵的正定和负定

矩阵Q正定的充要条件：
(1) Q所有的特征值大于0
(2) Q各阶顺序主子式都大于0
(3) Q各阶主子式都大于0
(4) 存在非奇异矩阵G，使得 \(Q = GG^T\)

矩阵Q半正定（正半定）的充要条件：
(1) Q所有的特征值大于等于0
(2) Q各阶主子式都大于等于0
(3) 存在矩阵G，使得 \(Q = GG^T\)

矩阵Q负定的充要条件：
(1) Q所有的特征值小于0
(2) Q奇数阶顺序主子式都小于0，偶数阶顺序主子式都大于0
(3) Q奇数阶主子式都小于0，偶数阶主子式都大于0
(4) 存在非奇异矩阵G，使得 \(-Q = GG^T\)

矩阵Q半负定（负半定）的充要条件：
(1) Q所有的特征值小于等于0
(2) Q奇数阶主子式都小于等于0，偶数阶主子式都大于等于0
(3) 存在矩阵G，使得 \(-Q = GG^T\)

关于更基础的一些概念：主子式、顺序主子式、余子式、代数余子式、伴随矩阵、方向导数与梯度等内容，自行回顾学习！

奇异、非奇异矩阵

讨论非奇异矩阵和奇异矩阵的前提：矩阵A是n阶方阵。

矩阵A可逆（非奇异）的判别方法（满足下列充要条件之一）：
(1) \(det(A) = \vert A \vert \neq 0\)
(2) \(Rank(A) = n\) 即满秩
(3) \(A\) 的所有特征值都不等于0
(4) \(A\) 可以表示成若干个初等矩阵的乘积（初等矩阵是可逆的）

矩阵A奇异的判别方法（满足下列条件之一）：
(1) \(\vert A \vert = 0\)
(2) \(Rank(A) < n\) 非满秩

非奇异矩阵就是可逆矩阵（满秩矩阵）。在数学上，“奇异”(singular)一词被用来形容破坏了某种优良性质的数学对象。对于矩阵来说，“可逆”是一个好的性质，表示该矩阵包含了其所能容纳的所有可用信息（不存在某几个行/列向量是线性相关的），即满秩。奇异矩阵行列式值为0，不可逆，等价于某个线性变换退化了，即变换之后有部分东西丢失了。

PS(PostScript):

A的充分条件是B（B是A的充分条件，条件是B，结论是A），
说明有了B就一定有A（充分性），
即由条件B可以推导出结论A。

A的必要条件是B（B是A的必要条件，即B是必要的），
说明没有B就一定没有A，
因为B是必要的（要作为结论），所以由A可以推导出B。

Reference: 矩阵可逆的几个充要条件

特征值与特征向量

定义：\(Ax = \lambda x\)，其中 \(A\) 是矩阵，\(\lambda\) 是特征值（也叫本征值），非零向量 \(x\) 是特征向量。\(A \cdot x\) 表示用矩阵对向量 \(x\) 进行一次线性变换（可以是拉伸+旋转，也可以只是拉伸或者只是旋转），而这种转换的效果就是一个常数 \(\lambda\) 与向量 \(x\) 的乘积（说明只进行了拉伸）。换句话说，就是对一个特定的矩阵 \(A\) 来说，总存在一些特定方向的向量 \(x\)，使得 \(Ax\) 和 \(x\) 的方向一样（未发生变化），只有长度改变了。这个长度的变化就是特征值的几何含义。

我们通常求特征值和特征向量就是为了求出在笛卡尔坐标系中，该矩阵能使哪些向量（当然是特征向量）只发生拉伸，使其发生拉伸的程度如何（特征值大小）。如果把矩阵看作运动，那么特征值就是运动的速度，特征向量是运动的方向。特征向量在一个矩阵的作用下作伸缩运动，伸缩的幅度由特征值确定（缩放因子）。旋转矩阵是没有实数特征向量和特征值的。这样做的意义在于，看清一个矩阵在哪些方面能产生最大的效果，并根据所产生的每个特征向量（一般研究特征值最大的那几个）进行分类讨论，可以作为主成分进行研究、减少计算量、降维等。

附：笛卡尔坐标系：正交坐标系，比如直角坐标系（坐标轴互相垂直）。笛卡尔空间中，任何一个点的位置由数轴上对应的坐标设定。

极大线性无关组

线性相关与线性无关

在一个线性空间中，如果一组向量 \(a_1, a_2, \cdots, a_s\) 是线性相关的，那么存在一组不全为0的数 \(k_1, k_2, \cdots, k_s\) ，使得 \(k_1a_1 + k_2a_2 + \cdots + k_sa_s = 0\) 成立。

如果 \(a_{j \ (j=1,2,\ldots,s)}\) 线性无关，则 \(k_1a_1 + k_2a_2 + \cdots + k_sa_s = 0\) 成立：当且仅当所有的 \(k_{j \ (j=1,2,\ldots,s)} = 0\)。

极大线性无关组

设A是一个n维向量组，如果从A中取出s个向量 \(a_1, a_2,\cdots, a_s\) 组成向量组，该向量组线性无关，且对于A中的其他任意向量b，都有 \(a_1, a_2, \cdots, a_s, b\) 线性相关，那么向量组 \(a_{j \ (j=1,2,\ldots,s)}\) 是矩阵（向量组）A的一个极大线性无关组，简称极大无关组。

矩阵的秩

小时候老师总是告诉我们：要有n个方程才能解出n个未知数。上了大学以后，我们知道这句话其实是不严谨的。如果你想确定的解出这n个未知数，只有n个方程是不够的，这n个方程必须都是“有用的”，也就是线性无关的才行，否则就会有某几个方程式表达重复（无用）的信息，相当于只是换了衣服而已，实质上还是同一个方程式，自然就无法求解其对应的未知元。这些真正有用的方程式个数就是（系数）矩阵的秩。从这个角度，我们可以更好地理解什么是矩阵的秩（Rank）。

矩阵的秩，是矩阵中极大线性无关组的向量个数，也就是以此矩阵的元素作为系数的方程组中，线性无关的方程个数。从另一个角度说，秩是矩阵变换以后的空间维度，代表这个矩阵实际包含的信息量的多少。我们可以回顾一下初等变换的过程：对矩阵的行列式作初等行变换时，线性相关的向量（行）会被消去（成为0），即不含有用信息。

线性代数，主要就是研究n元1次线性方程组（某个问题）解的存在性（有没有答案？）和解的唯一性（答案是否只有一个？）。如果存在解，如何找到这个解或者所有解？一般的含有n个未知数和m个方程的非齐次线性方程组可以表示如下： \[ \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ \qquad \qquad \qquad \quad \vdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n = b_m \\ \end{cases} \]

若 \(n\le m\) ，则有以下结论：

1）当方程组的系数矩阵A的秩：Rank(A) 与方程组增广矩阵 (A, b) 的秩：Rank(A, b) 相等，并且都等于未知元个数 n 时，方程组具有唯一解；

2）当方程组 Rank(A) = Rank(A, b) < n 时，方程组有无穷多个解；

3）当方程组 Rank(A) < Rank(A, b) 时，无解。

结论(1)很好理解，方程组里所有方程式互不冲突，m = n，信息一一对应。结论(2)，方程组里所有方程互不冲突，但是 m < n，存在自由变量可以随意取值（约束不够），因此具有无穷多解。结论(3)，存在多个方程式有冲突，信息有互斥的成分，存在 "0 = c" 的现象，自然无法求解。

另外，根据克拉默法则：

1）当系数矩阵A的行列式值：det(A) = 0 时，线性方程组（齐次或非齐次）要么有无穷多解，要么无解。

2a）对于齐次线性方程组（\(b_i = 0\)）来说，det(A)不等于0时，只有零解；det(A)等于0时，有0解和非0解。

2b）对非齐次方程组（上式）来说，det(A)不等于0时，有唯一解；det(A)等于0时，有无穷多解或没有解。

参考：如何理解矩阵的秩？

矩阵的行列式和迹

矩阵（方阵）A的迹：trace(A)，是矩阵A所有特征值之和。对 \(n \times n\) 的方阵A而言，迹等于A所有主对角线上的元素之和。

矩阵（n阶方阵）A的行列式（determinant）的值：det(A)，是方阵A全部特征值的乘积。行列式描述的是一个线性变换对欧几里得空间（线性的，可以用加法和数乘表示空间中所有元素；内积空间，可以用内积表示空间向量的角度信息（一定是赋范空间）；维度有限）中“体积”造成的影响。因为特征值是在特征向量方向上放缩的程度，可以认为特征值构成了特征空间的“骨”，类似于多面体的“边”、“高”等信息，当这些特征值相乘时，可以粗略的类比为体积的概念。